You want to solve Sudoku on your own? Try to solve Valid Sudoku (LeetCode 36) first. For Valid Sudoku, the initial guess is to create three functions for checking row, column, and box validity. But this is time-consuming because every time you check a number, you iterate over 9 elements of a row, 9 of a column, and 9 of a box.
The best way of solving this is to maintain storage (sets) for all 9
rows, 9 columns, and 9 small 3x3 boxes. Suppose you are placing a
number at coordinates (i, j).
Then check the set of the ith row if the number is
present or not.
Same for the jth column.
But for boxes, how do you determine which coordinates
(i, j) correspond to which box? It was simple for rows
and columns, since these were simple dictionaries with keys as
0,1,2,... and values as empty sets initially.
For boxes, what should the keys be?
Convert the coordinates (i, j) to
(i//3, j//3) and this new coordinate pair will be the
key. So the boxes are basically
(0,0), (0,1), (0,2), (1,0), (1,1), and so on.
PS: I solved the box check using this only, but the most famous
approach is to convert the (i, j) coordinate into a
single index like (i//3)*3 + j//3. This gives you an
index from 0 to 8. You can also do i//3 + (j//3)*3 It
just changes the direction of numbering of boxes from left-to-right
to top-to-bottom, which is not significant.
All set , Let's go for the Sudoku solver now.
Sudoku Solver
This question is really easy because there is no complex algorithm here it's just simple brute force + recursion + backtracking.
For any question where you need to explore many possible states with some constraints, recursion is your way (ignoring DP optimization). The function calls itself repeatedly until the base case is hit or the constraints are invalidated.
If the base case is hit - congrats, you have solved the problem (here)
If the constraints are invalidated you need to backtrack i.e , undo the move or go back to the previous guess to try a different option.
In this question, the base case is when there are no
. (empty cells) left.
If you have filled all . with numbers without
invalidating Sudoku, then obviously you have solved the problem.
How It Works Step-by-Step
Just like Valid Sudoku, maintain storage for all three: rows, columns, and boxes.
For every digit from 1 to 9, check if the digit is valid by checking the storage set of the particular row, column, and box.
If the digit is valid to be placed in the place denoted by
., place the digit and add it to the storage sets for
the row, column, and box.
Call the function again recursively to solve the next empty cell.

In the picture , the solve function is called recursively and the code waits or is blocked here until the recursive calls return something.
Understanding the Recursive Call Stack
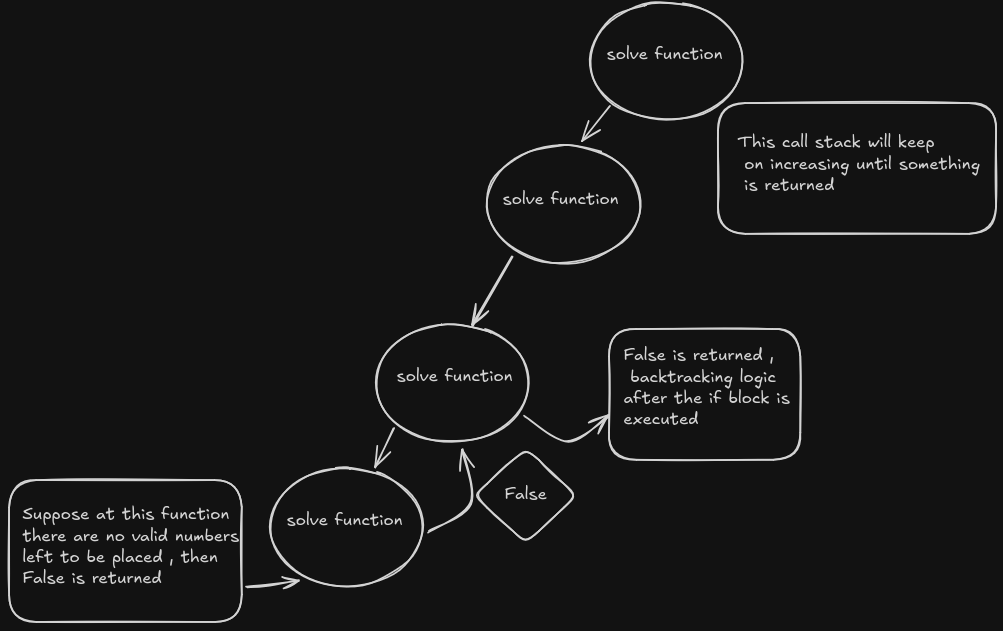
If in the recursive call stack, there are no digits valid to be placed, that means somewhere you made a wrong guess earlier.
Then the return False statement triggers backtracking.
So, where do we place the backtracking logic?
After the if solve() block
The backtracking logic includes removing that particular number from
the row, column, and box sets, and placing . back in
the board undoing your changes.
When Does the Function Return True?
The function returns True only when the base case is
hit i.e., no . left on the board.
When return True is called, the
if solve() checks become True, which then
start returning True up the recursive call stack,
indicating a fully solved Sudoku.
End
I don't expect anyone to learn recursion and backtracking with a single question, but the basic template is the same.
Don't try to visualize the entire recursive call stack; your brain can't comprehend.
Try solving by hand with pen and paper once; after a few problems, you'll get used to following the recursive backtracking template.
Well this was the most famous LC hard (in my college atleast ) following with N-queens , Aggresive Cows etc . I have some more blog ideas but gotta focus on websockets rn bye !